When dealing with multivariable real functions, we define what is called the partial derivatives of the function, which are nothing but the directional derivatives of the function in the canonical directions of \(\mathbb{R}^n\).

\partial command is for partial derivative symbol

Computationally, when we have to partially derive a function \(f(x_1,…,x_n)\) with respect to\(x_i\), we say that we derive it “as if the rest of the variables were constants”. This derivative is then denoted by:

\(\displaystyle \frac{\partial f}{\partial x_i}\)

that is, as a usual derivative but with “curly d’s”. The partial derivative symbol is generated in LaTeX with the command \partial, so that the previous equation was produced with the code:

% Partial derivative symbol in LaTeX
\[
   \frac{\partial f}{\partial x_i}
\]

Typeset complex equations with partial derivatives

If you have to deal with several partial derivatives along with your document, it is not practical to have to write every time fraction with the corresponding \partial symbols. It would be better to define a command that you passe only the function and the variable with respect to which we want to derive.

Instead of doing this work manually, the external package derivative is written by Simon Jensen already provides a set of commands which makes writing ordinary and partial derivatives of arbitrary order much easier. Additionally, this package provides a set of commands to define “variants” of the aforementioned derivatives.

1. Basic usage of \pdv command

We will not explain in detail all the capabilities and tools this package provides; instead, we will focus on the \pdv command, used to produce partial derivatives. This command takes several possible mandatory and optional arguments:

\pdv*[key-val]{function}/{variables}_{point1}^{point2}

Let’s see what they mean. We will start with the most important ones, and the only mandatory arguments:

• function determines the function which will be differentiated, and
• variables is a list of comma-separated variables whose purpose is to typeset the variable in which the function is differentiated with respect to.

For example, the output

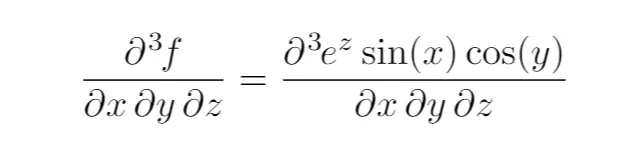
is produced with the code:

% Simple method to typeset complex partial derivatives
\documentclass{article}

% Required package
\usepackage{derivative}

\begin{document}

\begin{equation}
   \pdv{f}{x,y,z}= \pdv{e^{z}\sin(x)\cos(y)}{x,y,z} 
\end{equation}

\end{document}

2. Write function next to the fraction in partial derivative

Now let’s see what the optional arguments do:

• First we have the asterisk *, which determines where the function is typeset. If the asterisk is not present, the
  function is typeset in the numerator of the fraction, as in the previous examples. If instead the asterisk is present, the function is typeset next to the fraction.

Compare the two outputs:

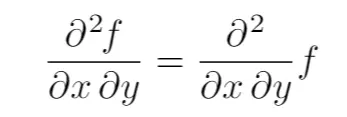
produced with the following LaTeX code:

% Typeset partial derivatives with inline function in LaTeX
\documentclass{article}

% Required package
\usepackage{derivative}

\begin{document}

\begin{equation}
   \pdv{f}{x,y}=\pdv*{f}{x,y}
\end{equation}

\end{document}

The optional argument inside square brackets is used to set the options of the derivative passing it a list of key and value pairs. There are a lot of options that can be specified, and if you want to explore them feel free to look at the package documentation.

3. Partial derivative order

Probably the most interesting one, that can save you some work, is order. This option can be passed a list of values inside braces, separated by commas, that determine the order with respect to which each variable should be differentiated. For example:

% Typeset partial derivatives with order in LaTeX
\documentclass{article}

% Required package
\usepackage{derivative}

\begin{document}

\begin{equation}
   \pdv[{2,3,5}]{f}{u,v,w}
\end{equation}

\end{document}

produces the following output:

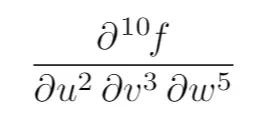
Be aware that this option is only available from version 1.0 of the derivative package.

4. Fraction style in partial derivative expressions

The fourth argument is an optional slash / written between the function and the variable arguments. It determines which fraction style the derivative is typeset with. Here you can compare the two styles:

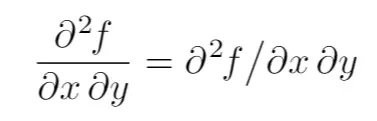
which is produced the following code:

% Fraction style in partial derivative
\documentclass{article}

% Required package
\usepackage{derivative}

\begin{document}

\begin{equation}
   \pdv{f}{x,y} = \pdv{f}/{x,y}
\end{equation}

\end{document}

5. Evaluate a partial derivative at a point

The last optional argument is _{point1}^{point2}, which specifies the point or points of evaluation, or also the variables held constant (a notation used mostly in thermodynamics). These points are typeset like a subscript and a superscript, respectively, of big parentheses around the partial derivative:

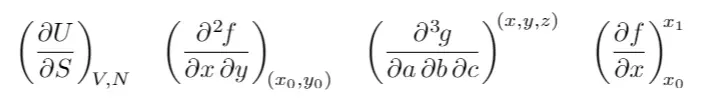
to typeset these derivatives, the lines of code were used:

% Evaluate a partial derivative at a point
\documentclass{article}

% Required package
\usepackage{derivative}

\begin{document}

\begin{equation}
    \pdv{U}{S}_{V,N}\quad
    \pdv{f}{x,y}_{(x_0,y_0)}\quad
    \pdv{g}{a,b,c}^{(x,y,z)}\quad
    \pdv{f}{x}_{x_0}^{x_1}
\end{equation}

\end{document}

We reached the end of this tutorial, If you have any remarks or suggestions, please feel free to reach us via email at admin@latex-tutorial.com